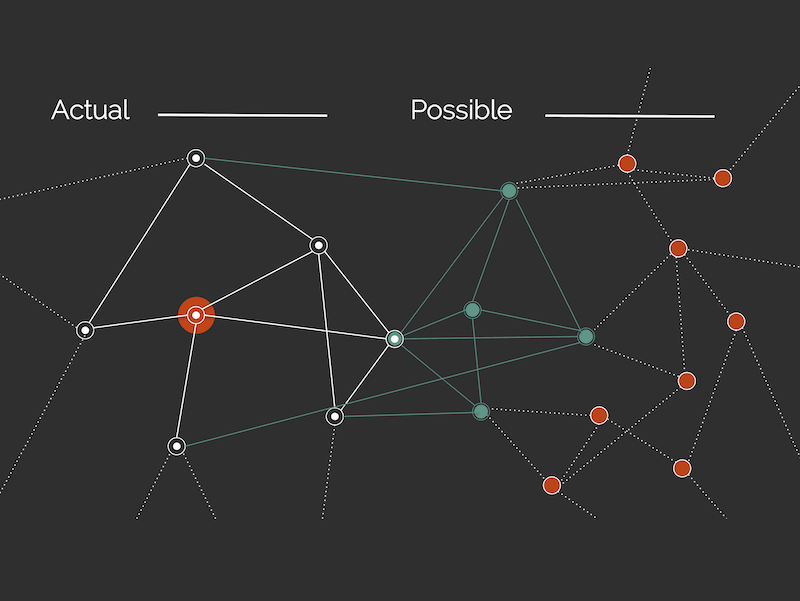
In this work, the authors developed a minimal model to describe the birth and evolution of social networks in three diverse social contexts: the network of mentions between Twitter users, the co-authorship network of the American Physical Society journals, and a mobile-phone-calls network. This task is of utmost importance, as social interactions represent the backbone of our societies. Besides, understanding the mechanisms that people apply when choosing how to allocate their social interactions can explain how our social organisation emerged. Many models tried to catch the underlying mechanisms driving the establishment and expansion of social connections networks. However, all of these models feature two main drawbacks: i) they are mainly growing models of a network -i.e., they do not account for the dynamics of the network itself- and ii) they require to fix some data-driven heterogeneous distribution to reproduce the real-world heterogeneity of given observables. For instance, people’s different propensity to socially interact is usually modelled assigning a fitness parameter to each node. Another example is that many models superimpose the mechanism that people apply to select their next communication alter with data-driven probability functions. To overcome these limitations, the authors propose a model building on the notion of Adjacent Possible. They assume that the social space that people explore is composed of three regions: the actual (i.e., all the connections we already experienced in the past), the adjacent possible – accounting fo all the people that are just one step away from the people we currently know- and the unknown, i.e., all those alters that we cannot encounter yet.
In detail, the model represents each person as an Urn Model with Triggering (UMT). This urn contains tokens whose IDs are the ID of other people in the network, that is, each urn has a unique ID, and every urn contains the IDs of other people. Each time an urn i gets active (proportionally to its size), it randomly selects an ID j from its collection and interacts with that user. This corresponds to an i -> j interaction event, mimicking the sequence of contacts that we find in common datasets logging human interactions.

Fig. 1 The different model steps: each column corresponds to a possible evolution step of the model, while each row displays a different aspect of each evolution step. On the top row, we show the composition of the urns, with the ball being drawn circled in red (rectangles, IDs of each urn are shown in their bottom right corner). The middle row shows the equivalent network representation of the system and how it changes within the evolution step. The bottom row shows the sequence event being logged at the time step t.
After their interaction, and regardless of their status, the two users reinforce their link, by putting back ρ copies of each other’s ID in their urn. Then, supposing it is the first time the two IDs get in contact, they exchange a so-called memory-buffer, a set of ν+1 IDs they select from their urn. The nodes propose these possible connections to their alter as their representative set of IDs. The authors implemented several strategies to choose this particular buffer and found that some strategies better describe different social contexts.Moreover, they found that a different balance of the reinforcement the ρ parameter telling how much to strengthen a connection activated thus increasing its probability to be re-activated in the future) and the novelty (the ν parameter telling how many balls to exchange when meeting a new alter) weights applies to these dataset. In particular, the APS resulted to be the most novelty driven network, while the Mobile Phone one is characterized by a stronger reinforcement of previously activated connections. The Twitter mention lies between the two, with a balanced influence of both the strengthening of old connections and the exploration of new one.
By applying these simple rules, and repeating them a sufficient number of times, the model generates a sequence of contacts. The latter describes the evolution of this synthetic social network. With the analysis of such dataset using network theory tools, the authors find that the model correctly reproduces many real-world network properties.

Fig. 2 The model’s scores: radar plots comparing eight selected observables measured in empirical (blue lines) and synthetic data (red lines). a) American Physical Society (APS) b) the 1-link subsampled APS c) the Mobile Phone Network (MPN), and, d) the Twitter Mentions Network (TMN).
To conclude, this theoretical model builds on the Adjacent Possible expansion and microscopic evolution rules that let emerge both microscopic and macroscopic features of real-world social networks without relying on unnecessary assumptions. On the macroscopic side, the model reproduces the main static and dynamic characteristics of the reference social networks: the broad distribution of degree and social activity, the average clustering coefficient, and the social innovation rate (i.e., how quickly a person expands her set of social contacts in time) at the global and local levels. It captures the probability for an individual with k active connections to acquire a new acquaintance at the microscopic level.

Read the article here